Master thesis proposal 2010-2011
Camera Calibration
 |
Advisors
| Edmond Boyer |
| LJK/PERCEPTION |
| E-mail: Edmond.Boyer@inrialpes.fr |
| Tel. : 04 76 61 53 54 |
Context
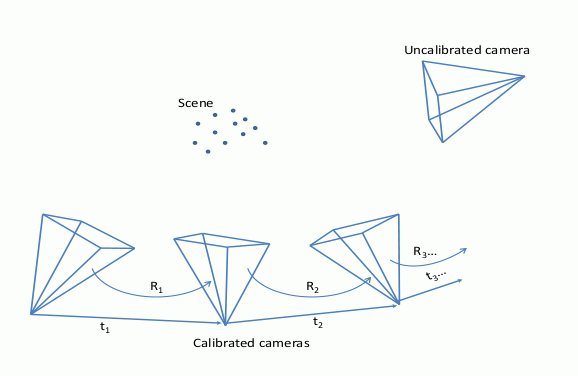
Camera calibration consists in recovering camera parameters, location and orientation for external parameters and focal lengths for internal parameters. It is a necessary preliminary step to many computer vision methods that involve several cameras, in particular 3D modeling methods. Camera calibration has been extensively studied over the last 30 years and several solutions have been proposed, the most efficient ones being based on calibration patterns. Without such patterns it is still possible to perform calibration. In particular, calibration of two cameras for external parameters has seen some efficient algorithms using minimal information in recent times [Nister 04, Stewenius 05]. Efficient calibration of multi-camera systems, however, is still a challenging problem. Pairwise camera calibration techniques do not easily scale up to multi-camera systems owing to error prone and time consuming computations involving rotation matrices.
Objectives
The objective is to recover the parameters of a camera using a minimal set of point correspondences in other already calibrated cameras. The interest is to provide a flexible calibration solution that can adapt to a new, or a moving, camera, as frequently occur with multiple camera systems, or that can be used to iteratively calibrate a set of cameras. To this purpose, we propose a geometric formulation of the calibration problem that turns a pair of point correspondences into a second degree polynomial with camera parameters as unknowns. The calibration problem then boils down to solving a system of polynomials. Of particular interest in this context is the recent work of H. Li [Li 10] who is considering a different problem but proposes an algorithm that solves for a very similar polynomial system. The objective of this work is therefore to implement a solution based on this approach, to experiment this solution and to build on it and propose a flexible camera calibration tool.
Pre-requisites
Required skills include computer vision, algebraic geometry, linear algebra, numerical analysis.
Keywords: computer vision, camera calibration, algebraic geometry, minimal problems, geometric vision.
References
- [Nister 04] D. Nister. An efficient solution to the five-point relative pose problem. PAMI, 2004.
- [Stewenius 05] H Stewenius. Grobner Basis Methods for Minimal Problems in Computer Vision. PhD thesis, Lund University, Sweden, 2005.
- [Ameller 00] Marc-Andre Ameller, Bill Triggs & Long Quan. Camera Pose Revisited - New Linear Algorithms, 2000.
- [Li 10] Hongdong Li. Multi-View Structure Computation without Explicitly Estimating Motion. CVPR, 2010.
- [Martinec 07] D. Martinec & T. Pajdla. Robust Rotation and Translation Estimation in Multiview Reconstruction. CVPR, 2007.
- [Nelakanti 10] Incremental Calibration for Multi-Camera Systems, Anil K. Nelakanti, M2R Mosig GVR report, 2010.